不确定性概念最早在经济学领域产生,后来又在量子力学、信息论等领域广泛应用。目前很多研究人员结合各自研究领域对LCA的数据不确定性做了很多定义,收到广泛认可的Huijbregts将LCA数据不确定性定义为在生命周期评价的整个过程中由研究人员的主观因素、数据的不准确和模型的基本假设等所有因素对整个评价结果所带来的影响。
从LCA框架中可以知道数据不确定性可以分为四类,其来源也各有不同:研究范围和研究目的的不确定性是由系统边界确定、模型基本假设、研究目的是否明确等因素的不确定性造成的;列表分析的不确定性是由数据的选择方法和数据质量的不确定造成的;影响评价的不确定性是由标准化参考值、环境类型、权重系数选择的不确定性造成的;结果解释的不确定性是由研究者对评价结果分析的主管性造成的。
Weidema于1998年首先提出使用系谱矩阵来分析数据的不确定性。Maurice于2000年首次将定性方法与定量方法结合使用,对某燃煤电厂的发电量进行了数据不确定性计算。Huijbregts在2001年将数据的不确定性划分为缺失数据和不精确数据两种类型,并提出了解决不确定性的方案。2003年莫华在分析了数据质量指数法和不确定性模拟法优缺点的基础上首次提出将两种方法结合起来分析数据的不确定性,而郑源则在解决LCA中数据不确定性问题上引入了概率统计方法来解决。2005年Shih-ChiLo采用蒙特卡罗方法和贝叶斯推理通过对LCA中数据不确定性做定量分析来实现降低评价结果不确定性的问题。刘涛在2006年提出需要进行选择性分析并快速筛选对评价结果不确定性有意义的数据来解决LCA实施期间的数据比较多的问题。2008年RaymondR.Tan第一次提出了一种基于模糊矩阵的影响评价模型,用于评价清单数据的不确定性。2010年任丽娟将分析方法归纳为三类,进行了详细分析,并指出了各自的优缺点。2012年,黄娜提出LCA中列表数据质量的定量评价方法,称为CLCD-Q法,朱立宏对LCA过程中的不确定性进行了分析阐述,使用数据质量指标法建立概率分布。
通常收集数据的手段是没有统一标准的,收集到的数据质量也会参差不齐,这会对评价结果产生不可估计的影响。为了有效评价数据质量,需要构建一个合理的质量评价指标体系。数据质量指标就是这样一个指标体系,具体是指依据具体要求来选择一些具体指标作为评价来构建谱系矩阵和数据质量矩阵的方法。在生命周期评价中一般对数据相关性和数据可靠性来对数据的质量进行评价。具体的指标为数据的可信度、代表性、时间相关性、地理相关性、技术相关性。根据每个指标的特点和要求,将其分为5个不同层次构建矩阵,如表1所示。
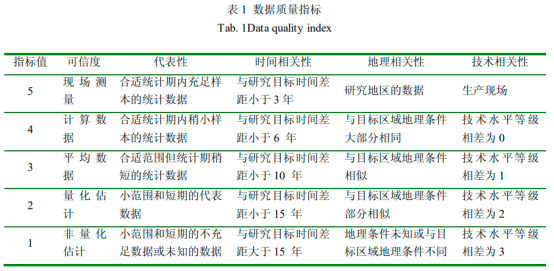
该方法在数据质量评价中应用广泛,其优点是可以根据所选评价指标和数据质量评价方便快速地比较每个指数的加权平均分发现数据质量问题;缺点是只能分析数据的不确定性,而不能评价结果的不确定性。
蒙特卡罗方法(MonteCarlomethod)是上世纪四十年代得益于科技发展和计算机的发明被提出的一种以概率统计理论为指导的重要数值计算方法,是一种使用随机数(或伪随机数)来解决计算问题的方法。MonteCarlomethod在金融学、经济学领域应用广泛,其本质是一种利用概率统计来模拟大量随机过程的数值方法,共分为三个步骤。首先需要将一个实际问题转化为对应的概率模型,并得出概率分布。在微积分中,求解类似:
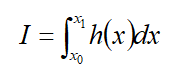
的定积分是,一般是先求得h(x)的原函数H(x),在用H(x1)-H(x0)计算定积分的值。但当h(x)非常复杂时,一般不能得到原函数H(x)的显示解,只能通过数值积分求解。数值积分求解一般是将积分区域分段,通过不断增加分段数来逼近真实解。当
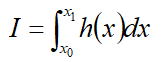
为了使其满足MonteCarlomethod,在求解时首先需要取一个概率密度函数f(x),使其在积分区域内满足:

就可以得到:
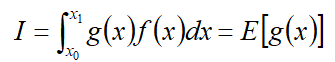
这样问题就变成了数学期望问题,通过求解g(x)的期望值就可以求解定积分。接下来是随机抽样。将一组在区间内服从均匀分布的随机数可以通过数学方法生成许多复杂分布的随机数来实现随机抽样。最后是计算估计量。设x1,x2,...xn,xn+1是从f(x)中抽取的子样,则I积分可近似为
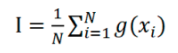
MonteCarlomethod可以有效评估数据的不确定性,目前主流商用LCA软件GABI、80Sim-Pro也都采用了MonteCarlomethod作为分析的主要方法。与DQI相比,MonteCarlomethod能够将输入、输出数据的不确定性进行量化,但缺点是在评价过程中没有考虑数据质量。
结合上面介绍的MonteCarlomethod和DQI特点,为了得到更高质量清单数据,可以结合两种方法使用。DQI、MonteCarlomethod相结合的方法首先需要根据数据质量矩阵要求对数据质量进行分析,然后根据评价结果采用对应的概率分布函数,最后使用两次MonteCarlomethod模拟量化得到所有数据和评价结果的不确定性,实施框图如1所示。
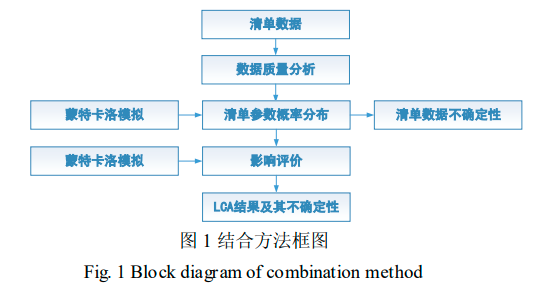
如前所述,依然选取5个指标作为数据质量评价的评估指标。每个指标又可得到5个分值,用每个指标的期望值代表数据的总分
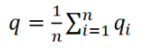
其中q代表数据质量的期望值,n代表质量指标数,qi代表各质量指标的得分,定义
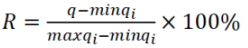
代表数据质量百分比,maxqi和minqi分别代表数据质量指标的最大和最小分值。这里选取了5个指标,因此数据质量向量共包含5个因子,由于1≤qi≤5,所以质量范围为4,可得:
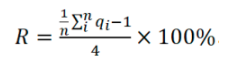 .
.
将表2中的每个值对应的DQI值分配给相应数据可见DQI值和R成正比。
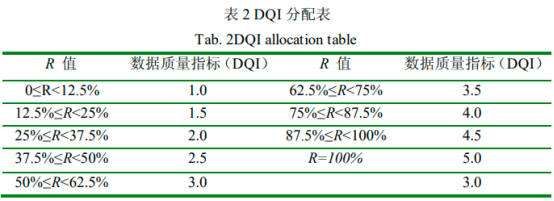
在对统计数据进行不确定性分析的一般步骤为:在统计样本中抽样,通过数值模拟得到概率密度分布函数,用相对标准差进行表征。在样本数量有限的情况下也可用概率分布模型来近似表征。Finnvedcn证明了在无法准确获取概率分布的情况下,最适合采用β分布,即
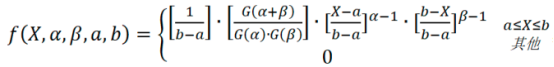
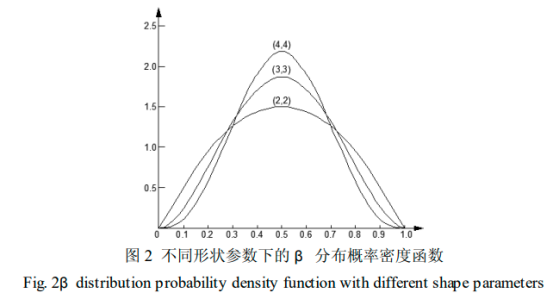
β分布是在2个端点参数a和b和2个形状参数α和β的控制下可以近似模拟出任何形状的分布。a和b限定取值范围,α和β决定了分布函数的形状,如图2所示。
本文首先介绍LCA的数据不确定性问题和研究现状,然后对比了数据质量指标法、蒙特卡罗方法、DQI和MonteCarlo相结合等三种数据不确定性分析方法,并对其优缺点进行了分析。