1992 年 Sony 成功开发出可充电的锂离子电池,由于电池工作电压高、体积小、质量轻、能量高、无记忆效应、无污染、自放电小、循环寿命长等优点,成为 21 世纪优越的能源载体。近年来,广泛应用于新能源汽车领域,如比亚迪、蔚来、特斯拉等。但是,所暴露的问题也相当严重,锂离子电池因为能量高,一旦发生爆燃,毁伤速度快,造成的损失较大。仅在 2021 年 1—5 月,国内共发生电动汽车起火事故 34 起,较去年同期增加 20起,涉及车辆数目 38 辆,较去年同期增长 73%,从各事故发生的车辆状态来看,使用状态中起火 20 起,占比59%,因此,准确判断锂电池健康状态,及时做出预警极其重要。
锂离子电池健康状态与自身容量息息相关,当衰减至初始额定容量的 70%时,电池会出现性能不稳定,严重时会导致电池发生爆燃。在追踪锂电池容量衰退即对电池剩余寿命(Remaining Useful Life, RUL)预测领域,国内外专家学者做出巨大的贡献。目前主要有两种方法:基于模型的方法和基于数据驱动的方法。基于模型的方法通过数学的方法建立模拟电池老化的模型,该方法建立的模型仅适用于某一特定种类和工况的电池,适用范围较为狭窄。而数据驱动的方法是基于统计学和神经网络理论,利用电池运行历史数据构建老化预测模型,该方法更容易应用在不同的场合。
目前,基于数据驱动的锂电池 RUL 预测方法主要是通过提取电池运行中参数构建健康因子,使用神经网络训练建立预测模型。潘海鸿等人采用极限学习机(Extreme Learning Machine,ELM)方法建立锂电池健康状态估算模型,然而在实际应用中,ELM 模型由于随机选择隐含层输入权值和阈值导致预测结果稳定性较差;曹孟达等人通过提取电池充电期间端电压、端电流等健康因子,使用深度学习的方法对锂电池 RUL 进行预测,但是在容量衰退后期,模型跟踪能力较差;杨战社等人[5]将容量作为健康因子,使用支持向量机的方法建立电池
RUL 预测模型,从预测结果看,模型跟踪能力还有待提高;史永胜等人将容量通过自适应噪声完全集成的经验模态分解为波动与趋势分量,然后对采用长短期记忆网络(Long Short-Term Memory,LSTM)建立各部分预测模型,从模型的预测结果看,容量跟踪能力较强,但是判定失效循环次数精度提高不明显;熊瑞等人利用长短期记忆递归神经网络学习锂电池容量退化的长期依赖性,但是这种方法无法跟踪锂电池容量再生现象。除此之外,NASA 电池数据集循环次数较少,B0005 号数据集仅 168 组,基于神经网络方法建立的模型,大都是对电池中后期容量衰退进行跟踪,电池早期容量跟踪也很重要,并且较少的训练数据集容易陷入局部最优值,难以衡量模型好坏,除了训练数据,测试数据也非常少,少量数据正确与否可能会对结果产生较大影响。
综上所述,为解决 ELM 网络随机选择隐含层输入权值和阈值导致预测结果稳定性较差的问题,使用樽海鞘群优化(salp swarm algorithm,SSA)的 ELM 方法构建具有全生命周期预测能力的 RUL 预测模型,同时针对训练数据集不足的问题,本文提出一种基于插值的方法增加训练数据集的容量。使用来自 NASA 研究中心的电池数据集,验证所提出模型的适用性能,并且与基于历史数据预测方法的结果进行比较,验证预测模型的有效性。
神经网络模型的学习能力与网络结构、网络初始权值的设定、算法种类以及训练数据集的规模息息相关,神经网络方法应用广泛,针对不同问题,选择合适的网络可以更好的进行学习,但是对于数据量本身就较少的问题,算法种类等提高模型学习能力的手段则不适用,因此,基于原始数据进行容量扩增是一种可行的办法。
1.1 Akima 样条曲线插补方法概述本文主要利用插补的方法进行数据集容量的扩充。目前插补方法主要有: Akima 样条曲线插补、C(CUBIC)样条曲线插补、贝塞尔(Bezier)曲线插补、PH(Pythagorean-Hodograph)曲线插补、B 样条曲线插补等,由于电池容量记录每间隔一次循环周期进行,各个循环之间容量变化大,为使曲线比样条函数插值曲线更光顺,更自然,因此选用 Akima 插补的方法。
Akima 非线性插值理论是由 Akima 教授于 1970 年建立的一种全新的光滑非线性插值方法,该方法所建立的曲线更光滑,过渡更自然,目前已被国内外广泛应用于测绘、遥感等领域。在二维平面上,取 4 个点连成曲线,分别为 A(xi-2, yi-2),B(xi-1 , yi-1),D(xi+1 , xi+1),E( xi+2, xi+2),此时要在 B 和 D 之间增加一点 C( xi, yi),根据 Akima 插补原理,需要根据其他数据点建立具有一阶导数的三次多项式曲线。C 与 D 之间的三次多项式为:
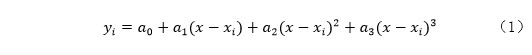
式中,的取值范围为( , ),a0,a1,a2,a3 为多项式系数。系数计算方法为:
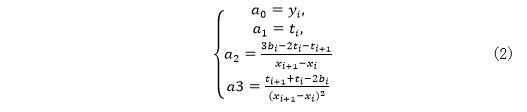
式中,为多项式曲线在数据点 C 的一阶导数, 为 CD 线段的斜率,根据 Akima 插补法的几何条件:
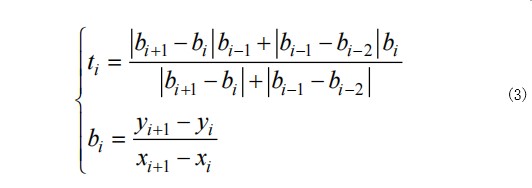
式中,bi-2,bi-1 ,bi+1分别是线段 AB、线段 BC、以及线段 DE 的斜率。根据公式 1 通过逐步取点插补,得到数据点之间的非线性光滑曲线,完成数据之间的填充。
锂电池在运行过程中,除电压、电流以及运行时间可以直接提取外,容量等表征电池性能的参数需要经过后期计算得到,程序较为繁琐,会降低 RUL 预测模型的实时性。此外,对于循环充放电的锂离子电池来说,在其放电过程中,电池两端的电压从一个相对高的电压下降到另一个相对低的电压需要一段时间,而该时间会随着电池充放电循环次数的增加而不断减少。因此,本文基于可直接提取的电池放电电压参数构建健康因子。在每一次放电周期过程中,提取电池处于低电压与高电压的时间,计算差值作为等压降放电时间。表达式如下:
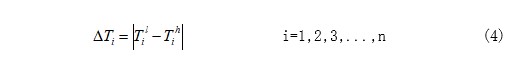
其中,为等压降放电时间, 为第i次循环低电压对应时刻, 为第i 次循环高电压对应时刻, n为锂电池循环最大次数。因此,等压降放电时间序列可以表示为:
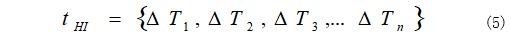
在这里,为实现锂电池全生命周期 RUL 预测,我们提取电池早期 30 次循环数据,利用 Akima 插补的方法扩充健康因子容量。
ELM 是一种单隐层前馈神经网络的学习算法,因为其模型简单,学习能力强,被广泛应用于健康状态的预测方面,ELM 算法的结构包括 3 层,分别为输入层、隐含层以及输出层,其结构如图 1 所示。
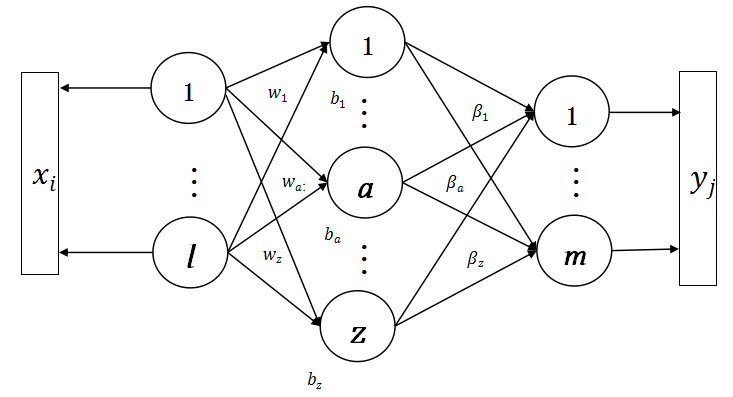
根据结构图,ELM 算法可以这样描述:
其中:
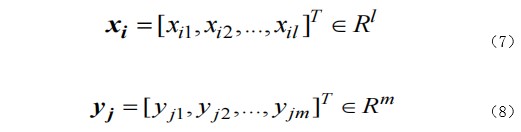
wi=[wi1,wi1,…,wi1]T为输入层到隐含层的权值,βi=[βi1,βi1,…,βi1]T是隐含层到输出层的权值,g(·)为隐含层激活函数,bi为隐含层偏差。则 ELM 网络的输出为:
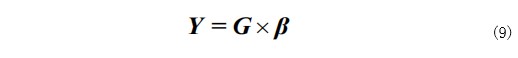
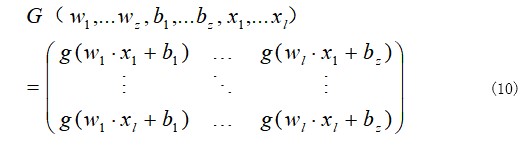
通过确定输入权重与隐层偏置,加载训练集,可以确定输出权重 β:

G+为矩阵的 Moore-Penrose 广义逆矩阵。得到β后,即完成了 ELM 的训练,然后使用训练集产生的 ELM模型对其余样本进行预测。
樽海鞘群算法是由 Mirjalili 等人在 2017 年提出的一种模仿樽海鞘群的群体行为的启发式算法。樽海鞘是一种小型的远海胶质脊索动物,身体呈半透明的桶状,多以海上漂浮植物为食。在海洋中成群存在的樽海鞘处于无性时期时,上十亿地聚集在一起形成樽海鞘链的链状结构,以“喷气式”方式运动。因此,樽海鞘的群体行为是“链条”的分布方式,领导者居于链条的顶端,跟随者紧密地彼此跟随从而进行链条式的食物捕捉和运动。假设樽海鞘群是由N 个 d维因子组成,即可用Nd维矩阵表示为:
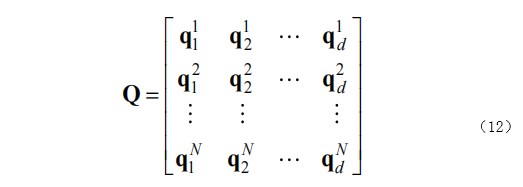
领导者的位置更新为:
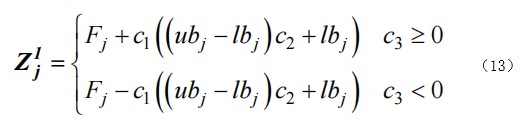
式中,Zi1为第一个领导者在第j维度时的位置,Fj为食物在j维的位置,ubj和lbj分别为上界和下界,c1、c2、c3为随机值。c2和 c3是处于[0,1]之间的随机值,c1的定义为:
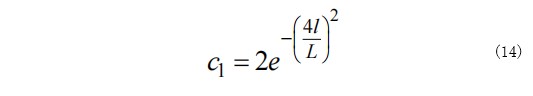
其中, 为最大迭代次数, 为当前迭代次数。其领导者位置更新利用牛顿第二定律为:
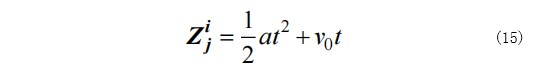
SSA 算法通过启动多个随机位置的樽海鞘开始逼近全局最优。然后它计算每个樽海鞘的适应度,找到适应度 最好的樽海鞘,并把最好樽海鞘的位置分配给变量,作为樽海鞘链要追逐的源食物。同时,系数c1使用等式更新。对于每个维度,使用等式更新前导樽海鞘的位置。并且利用等式更新跟随器樽海鞘的位置。如果任何樽海鞘超出搜索空间,它将被带回到边界上。除了初始化之外,以上所有步骤都被反复执行,直到满足结束标准。
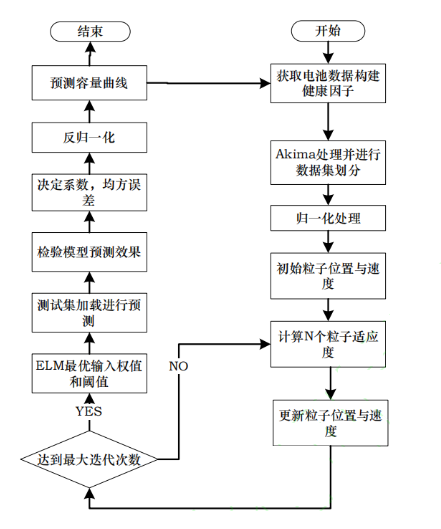
由于 ELM 在训练与预测过程中,输入权值和阈值为随机赋予,导致输出存在波动,预测结果不可靠,因此,提出将 SSA 和 ELM 方法融合,以优化选择输入权值和阈值,利用 SSA 的算法优化 ELM 网络,其中每个樽海鞘经过的路径代表一个候选 ELM 网络。为了实现这种表示,樽海鞘被设计用于保存要优化的网络参数,即保存输入层与隐含层间的连接权值和隐含层神经元的偏置值,使得锂离子电池剩余寿命预测结果精准可靠,同时,传统的利用一部分数据训练得到的模型,在电池容量预测后期会发生偏离,这是因为锂离子电池在运行过程中工况等外部条件会发生变化,模型需要学习得到最新的衰退趋势,因此,提出滚动更新的 RUL 预测模型,即将最新 运行的电池容量以及健康因子信息加载进入训练数据集,删除电池早期运行数据,重新训练模型,使模型获取最新的容量衰退趋势。具体的预测流程如图 2 所示。
1) 初始化网络参数。设置种群数目以及搜索空间的上下界,确定 ELM 算法隐含层节点数目和最大迭代次数;
2) 选取电池运行的历史数据,最近的若干个循环的健康因子为模型的训练输入量,容量为训练输出量。
3) 以适应度函数为食物源,对每个樽海鞘的位置进行排序,获取最优适应度的位置,并更新领导者和追随者;
4) 对模型进行训练,获取全局最优适应度值,得到基于 SSA-ELM 循环更新的锂离子电池 RUL 预测模型,并进行预测,重复步骤 24,建立具有滚动更新的 RUL 预测模型。
对模型进行两种方式的评价,分别为预测循环次数的准确性和容量衰减跟踪的效果。使用平均绝对误差(mean absolute error,MAE) 和均方根误差(root-mean-square error,RMSE)作为评估标准:
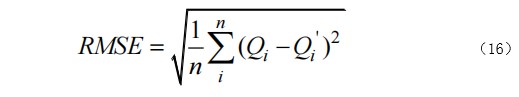
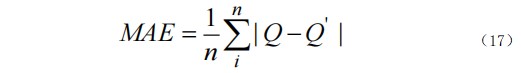
式中, Qi为真实值,即锂离子电池实际容量;Q'i为预测容量值;n为循环次数。
当锂离子电池的容量降至失效阈值时,循环次数的实际值与预测值之间的误差定义如下:
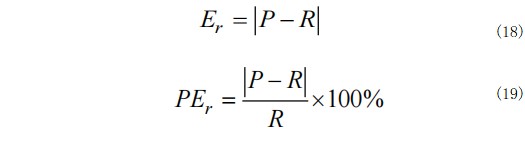
其中P为预测循环次数,R为实际循环次数。
本文选用 NASA 电池数据集 B0005~B0018,电池型号参数为额定容量 2Ah,额定电压 4.2V。在室温下以 1.5A的恒定电流模式进行充电,直到电池电压达到 4.2V,然后以恒定电压模式继续充电,直到充电电流降至 20mA以 2A 的恒定电流(CC)进行放电,直到电池 B0005、B0006、B0007、B0018 的电压分别降至 2.7V,2.5V,2.2V,2.5V。数据集包含的测量参数有:周期、环境温度、时间、电压、电流、容量、阻抗。当电池达到寿命终止标准时,即额定容量衰减 30%,实验停止。
分别对 B0005、B0006、B0007、B0018 组数据提取等压降放电时间,高位电压设置为 3.9V,低位电压设置 3.5V,提取 30 次循环数据得到训练数据集,并在后期进行实时更新,部分训练数据集如图 3 所示。
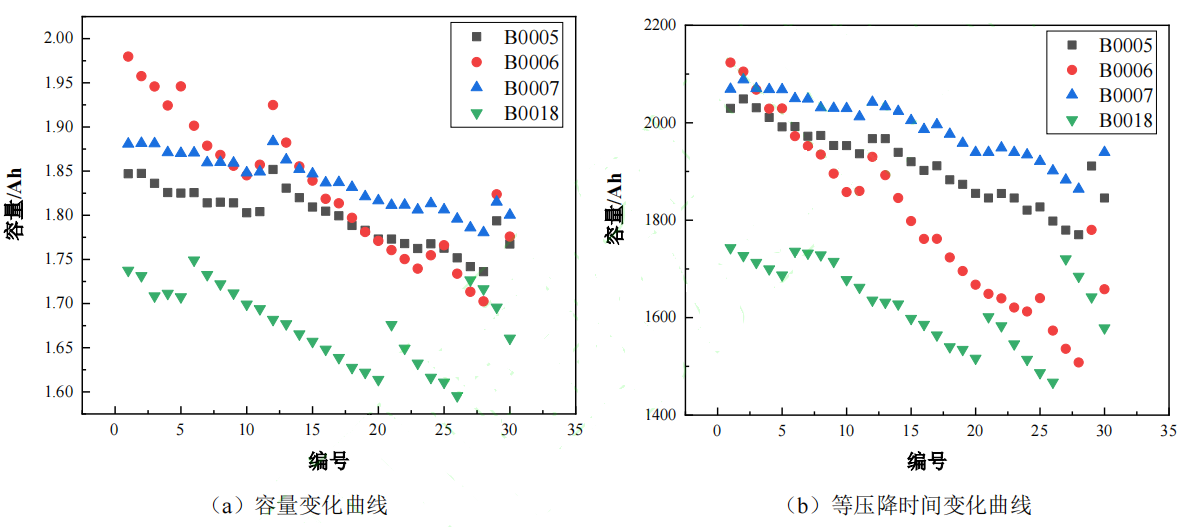
容量与等压降时间变化应该是散点图,在散点之间,通过 Akima 插补的方法对其进行填充,扩大训练数据集容量至 500 组。如图 4 所示。
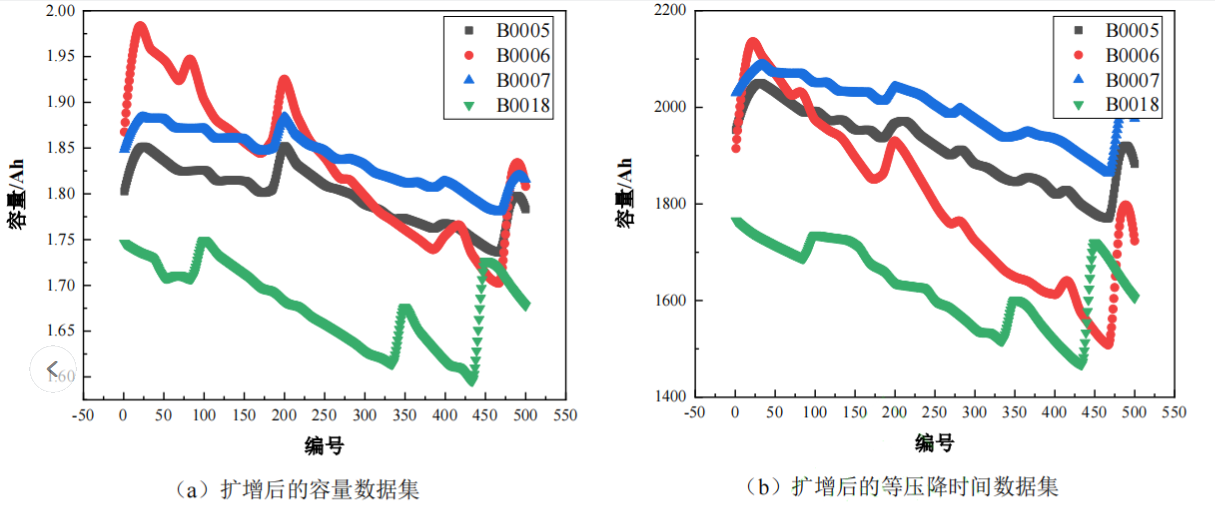
健康因子与容量数据间的相关性越高,则后期模型预测能力越强,对提取得到的健康因子与容量数据进行相关性分析,结果如表 1 所示。
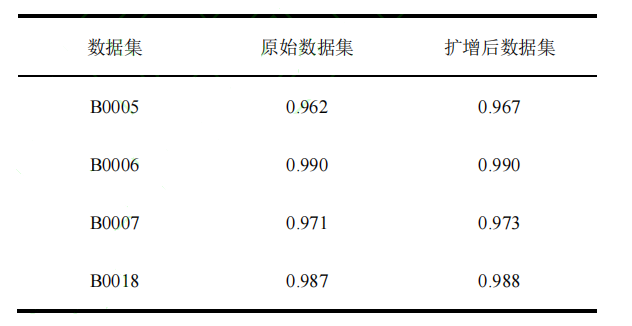
从相关性分析可以看出,扩增后的训练数据集相比原始提取的具有稍许优势,表明基于 Akima 扩增训练数据集的方法有效。
使用 MATLAB2019b 进行 SSA-ELM 模型的搭建,将 3.1 节获取的训练数据集加载进入 SSA-ELM 模型之中进行训练,得到的 RUL 预测模型。使用得到的模型对 B0005、B0006、B0007、B0018 四组数据进行预测,电池失效阈值为:1.4Ah,预测起点为第 30 次。并且与基于原始数据的 80 组训练数据集预测的结果进行对比,预测结果如图 5 所示,基于 RMSE、MAE 等指标进行模型评价,结果如表 2 所示。
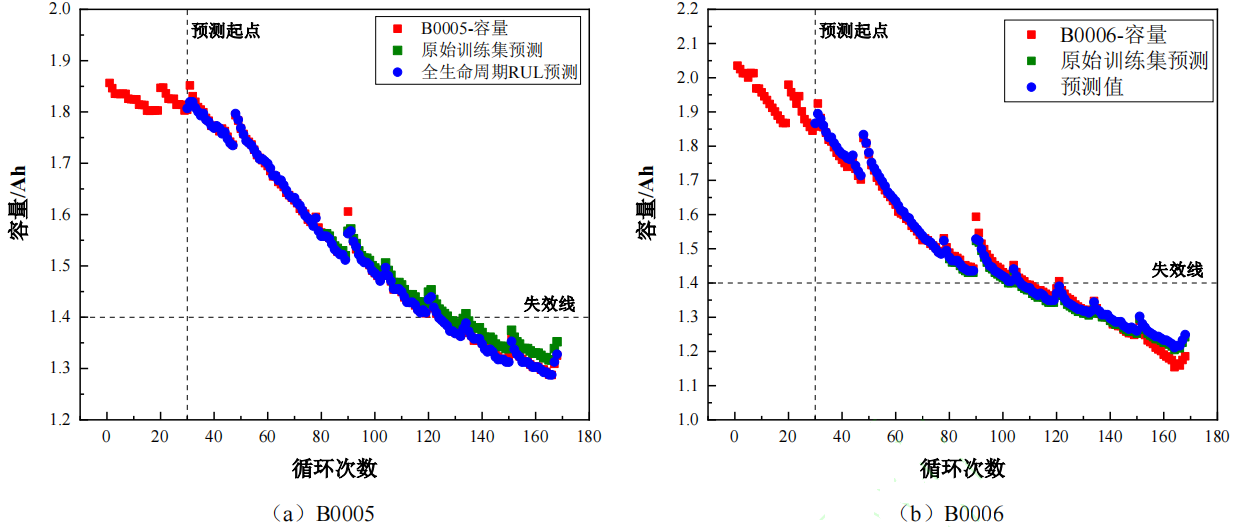
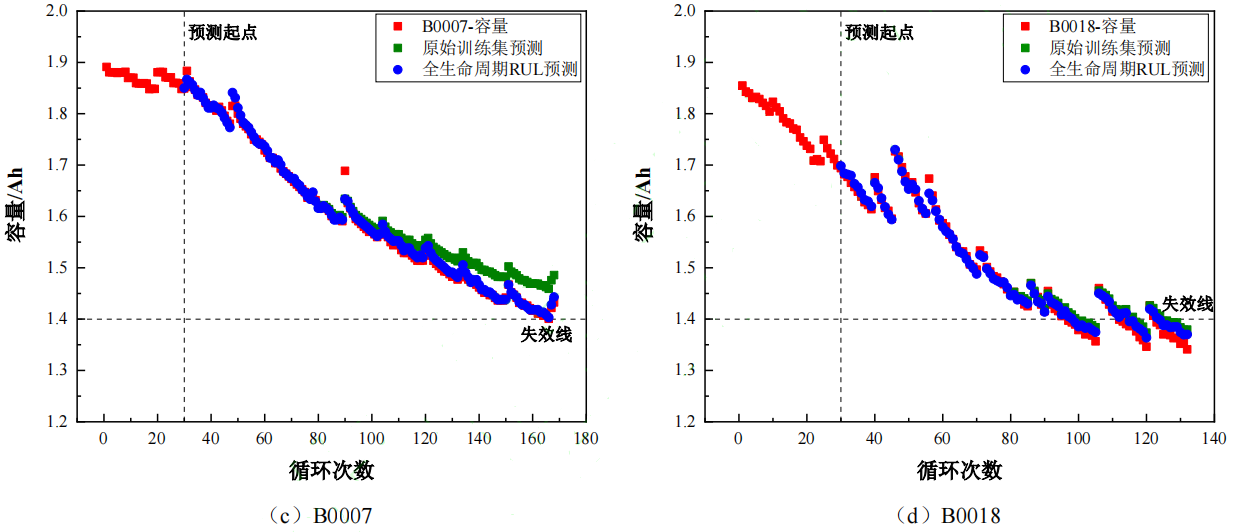
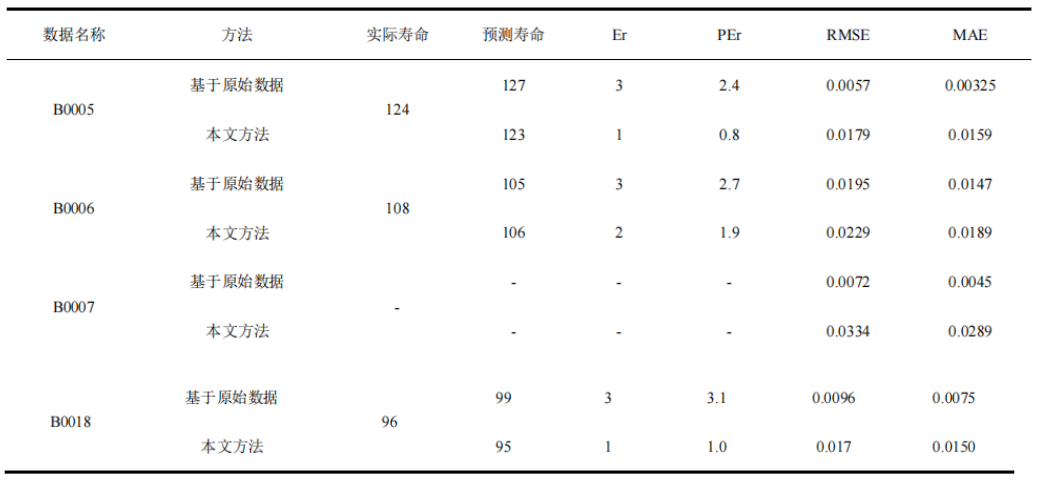
由于 B0007 号电池数据集未衰减至理论失效阈值,因此模型在这一情况下仅分析评价其跟踪能力。
通过评价指标可以看出,使用有限数据集进行锂电池 RUL 预测,无论是在容量衰退趋势跟踪方面,还是预测到达失效循环时的次数方面,误差均大于本文提出的基于 Akima 方法扩充训练数据集的方法,同时,本文还提出基于 SSA-ELM 的方法构建具有循环更新能力的锂电池 RUL 预测模型,进一步增强了模型在电池中后期的跟踪能力,提高了锂电池 RUL 预测结果的准确性和稳定性。
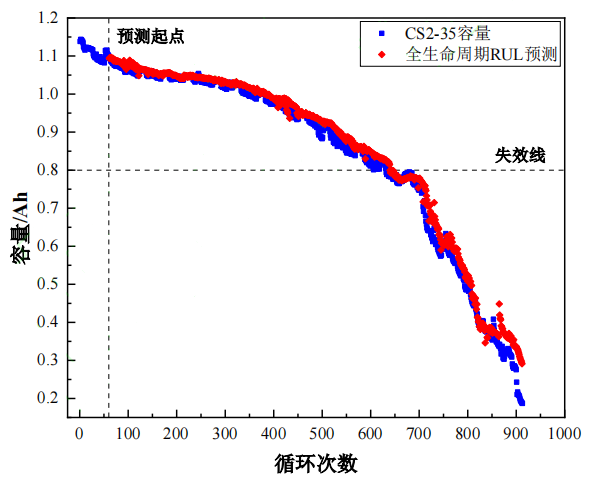
为了验证模型的适用性能,提出使用马里兰大学的电池数据集 CS2-35 号进行验证,其电池初始容量约为 1.1Ah,其循环模式为:以恒定电流 0.55A 充电至电压到达 4.2V,而后以恒压充电至电流下降至 0.05A 完成充电,之后以恒定电流 1.1A 放电至电池电压下降至 2.7V,此为电池的一个循环周期。如图 6 所示,为使用提出的预测模型进行验证的结果,经过计算,预测结果 RMSE 为 0.0263,MAE 为 0.0187 误差较小,得到的失效循环为 642,
实际的失效循环为 631,结果接近,表明所提出的预测模型有效。
本文提出了一种基于 Akima 插补方法进行训练数据集容量的扩充,并使用樽海鞘群算法对极限学习机的隐含层输入权值和阈值进行优化,建立具有循环更新能力的锂电池剩余寿命预测模型。通过 Akima 方法,解决了锂电池早期寿命预测数据量较少,无法追踪的问题,提高了模型的适应能力。基于樽海鞘群算法对极限学习机进行优化,解决了模型预测过程中不稳定的问题,同时,循环更新训练数据集的方法,通过去除旧的历史数据加载 新的运行数据,保证了电池寿命预测模型的跟踪能力,确保了中后期模型预测结果偏差较大的问题,与传统的基于历史数据进行电池剩余寿命预测的方法相比,所提出的方法具有全寿命周期剩余寿命预测的能力,和较高的准确性。